PDAFit¶
Photon Distribution Analysis (PDA)¶
General introduction to PDA¶
Photon distribution analysis (PDA, [Antonik2006] [Nir2006]) is a statistical method to describe the observed shot-noise limited FRET efficiency histograms by means of the underlying distance heterogeneity. PDA explicitly takes the statistics of photon emission and experimental correction factors into account and achieves higher accuracy than a direct analysis of the FRET efficiency histogram. It is especially useful for identifying heterogeneity in the FRET efficiency distribution that exceeds the expected value from shot-noise alone, allowing to quantify how defined a conformational state is.
PDA targets the uncorrected FRET efficiency histogram (also called proximity ratio histogram, PRH), where the proximity ratio is given by:
The algorithm simulates an expected proximity ratio histogram based on the input distances, correction factors and observed distribution of total photon counts, which accounts for the shot-noise. By variation of the parameters of the distance distribution, one can find the parameters that best describe the data.
Generally, two approaches have been proposed to simulate the proximity ratio histogram. Seidel and coworkers developed an analytical approach to calculate the PRH [Antonik2006], while Weiss and coworkers used Monte Carlo simulations to generate an approximate PRH [Nir2006]. Both approaches are implemented in the software, together with a related approach based on a maximum likelihood estimator.
Generally, the proximity ratio histogram is given by:
Here \(P(N)\) is the photon count distribution, i.e. the probability to detect \(N\) photons, and \(P_E(N_{GR}|N)\) is the probability to detect \(N_{GR}\) red photons out of \(N\) total photons, given the apparent FRET efficiency \(\epsilon\), described by a binomial distribution:
The apparent transfer efficiency \(\epsilon\) is hereby a function of the correction parameters. Background photon counts are additionally considered as described in the references.
The model function¶
PDAFit currently only supports normal distributions of distances with up to 5 states. The model additionally allows the inclusion of a donor-only population, which will behave differently from a low FRET population since no direct excitation of the acceptor dye can occur. Generally, the model function takes the form of:
I.e. the donor-only fraction is equivalent to the total percentage of donor-only molecules, while the species fractions \(F_i\) yield the fractions among the double-labeled molecules.
If no conformational heterogeneity is present in the sample and the broadening of the distance distribution is solely due to photophysical artifacts, the observed distribution width \(\sigma\) is proportional to the center distance \(R\) [Kalinin2010b]. Select the Fix Sigma at Fraction of R checkbox in the Settings tab to activate the constraint \(\sigma = f*R\), where \(f\) is the fraction. You can either leave the fraction as a fit parameter or fix it by checking the Fix checkbox next to the edit box.
Generating PDA data¶
For efficient calculations, PDA requires the data to be of equal time length. Thus, instead of performing the analysis on burst-wise data, the individual bursts are sectioned with a constant time window (typically 1 ms). As a consequence, the obtained proximity ratio histogram in PDAFit may look slightly differently from the histogram in BurstBrowser.
The process of exporting data from BurstBrowser for use in PDAFit is described here.
The correction parameters¶
The correction factors used in PDAFit mostly resemble the correction used in BurstBrowser (see correction factors there). If corrections have been applied in BurstBrowser, these are transferred to PDAFit. You can inspect the correction factors in the Parameters tab.
An exception to this rule is the direct excitation factor. In burst analysis, this correction factor is based on the signal in the direct acceptor excitation channel and thus dependent on the acceptor laser power. However, PDA requires the probability of direct acceptor excitation by the donor excitation laser \(p_{de}\), which is given by:
Here, \(\epsilon_{D/A}^{\lambda^{ex}_D}\) is the extinction coefficient of the donor or acceptor at the excitation wavelength of the donor fluorophore. This quantity has to be determined for each dye pair and is not accessible from the burst data.
In addition to the correction factors, the bin size of the loaded PDA file is given Bin [ms]. This parameter can not be modified. To change the bin size, export the data again from BurstBrowser with a different time bin.
When working with multiple files, you can use the All row to change the respective parameter for all files.
Note
The calculated histogram library is dependent on the set correction factors. A change in any of the parameters will trigger a recalculation of the histogram library, which can be time consuming. Set the parameters correctly in the beginning to save time.
Data selection¶
By default, the whole data set is selected. The selection can, however, be restricted in PDAFit using the left column in the Settings tab.
- Minimum number of photons per bin:
- Set this to a value larger 0 to exclude low photon number time bins from the analysis.
- Maximum number of photons per bin:
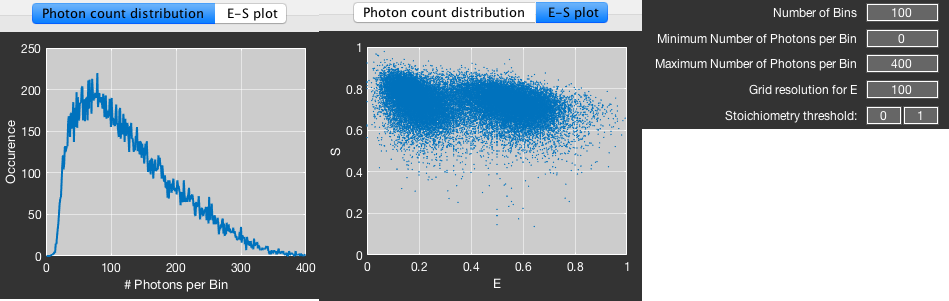
- This will limit the maximum number of photons per time bin. The computation time for the histogram method scales with the maximum number of photons per time bin, which makes it beneficial to limit this number, especially if only a few time bins contain a large number of photons, Inspect the photon count distribution to select a reasonable value for this parameter. (The other fit methods do scale mainly with the number of bursts and are mostly independent of the number of photons per time bin.)
- Stoichiometry threshold:
- Additionally, you can limit the allowed stoichiometry range as seen in the Efficiency vs. Stoichiometry plot (E-S). The displayed stoichiometry is calculated based on the raw photon counts \(S=\frac{N_{RR}}{N_{GG}+N_{GR}+N_{RR}}\).
Applied selection criteria are globally applied to all loaded data sets.
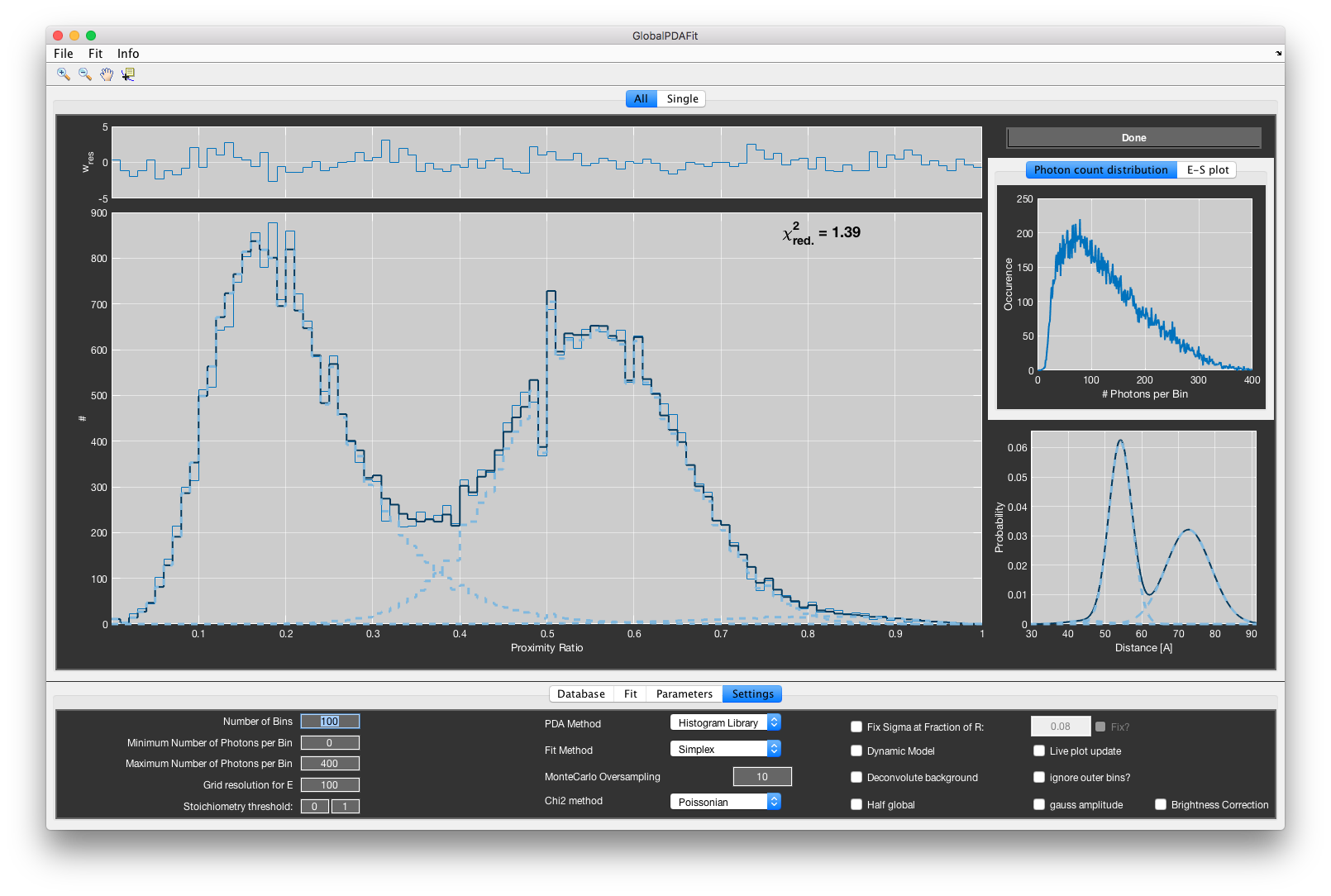
The All and Single tab¶
The All tab displays all loaded data sets simultaneously. Select the Single tab if you want to inspect a single data set alone. Use the popup menu located in the bottom right of the Single tab to select the data set to be displayed. When the Single tab is active, only the selected data set will be fit.
Performing a PDA fit¶
After setting all correction parameters and initial fit parameters, click Fit -> Start in the menu. If no global parameter is specified, the program will fit the data sets one after the other. If global parameters are considered, the total chi-squared over all data sets is minimized. At any point, you can stop the fit routine by selecting Fit -> Stop. To set good starting parameters, you can preview the histogram based on the currently set model parameters by selecting Fit -> View.
Once the fit is finished, you can store the fit result in the data files by selecting File -> Save to Files(s). To obtain figures of the result, select File -> Export Figures. This will store the result in a subfolder of the data file.
PDA fit methods¶
Histogram Library¶
The Histogram Library fit methods implements the PDA method developed by [Antonik2006]. The algorithm generates shot-noise limited histograms for a grid (library) of equally spaced apparent efficiency values over the interval [0,1]. The setting Grid resolution for E in the Settings tab determines the number of sample points over the interval (set this to at least 100). To implement the distance distribution model, the probability distribution of the distance is transformed into efficiency space. The simulated histogram is then a probability-weighted linear combination generated from the histogram library.
The advantage of this approach is that an accurate histogram is generated. After the initial preparation period, during which the histogram library is generated, the computational load is minimal, since only linear combinations have to be computed.
The accuracy, especially at the extreme edges of very small or large distances, is limited by the resolution of the grid of efficiency values of the histogram library. Especially if the fitted distance distribution show a very narrow width (\(< 1\:\mathring{A}\)), the grid resolution should be increased. As an example, at vanishing distribution width \(\sigma \rightarrow 0\:\mathring{A}\), the algorithm will not find the true value of the center distance, but instead the distance value that belongs to the closest efficiency value of the grid. This effect of the grid, however, is reduced for normal distribution width \(\sigma > 2\:\mathring{A}\), where the resulting histogram will be a weighted linear combination of multiple library elements.
MonteCarlo¶
The MonteCarlo method uses the algorithm as proposed by [Nir2006] to simulate the proximity ratio histogram. Hereby, for every data point, a random number generator is used to draw a value for the proximity ratio. To reduce stochastic noise, set the MonteCarlo Oversampling parameter in the Settings tab. Oversampling will repeat the histogram generation for the specified number of times and return the average.
The MonteCarlo method operates on a continuous parameter space and does not suffer from the problems associated with the gridding for the Histogram Library method. It can be slower than the other methods, depending on the desired accuracy as determined by the oversampling factor.
Maximum Likelihood estimator¶
The MLE method does not rely on the simulation of a histogram and thus completely avoids the necessity to bin the data. Instead, it computes the likelihood that the model parameters may produce the data directly. As such, no live plot update is possible. The fit result is finally displayed by means of simulation by the MonteCarlo method.
The MLE method, as the MonteCarlo method, operates on a continuous parameter space without any gridding. It generally shows a smoother optimization surface than the other two methods, and is thus suited well to be used with gradient-based fit algorithms.
Dynamic-PDA¶
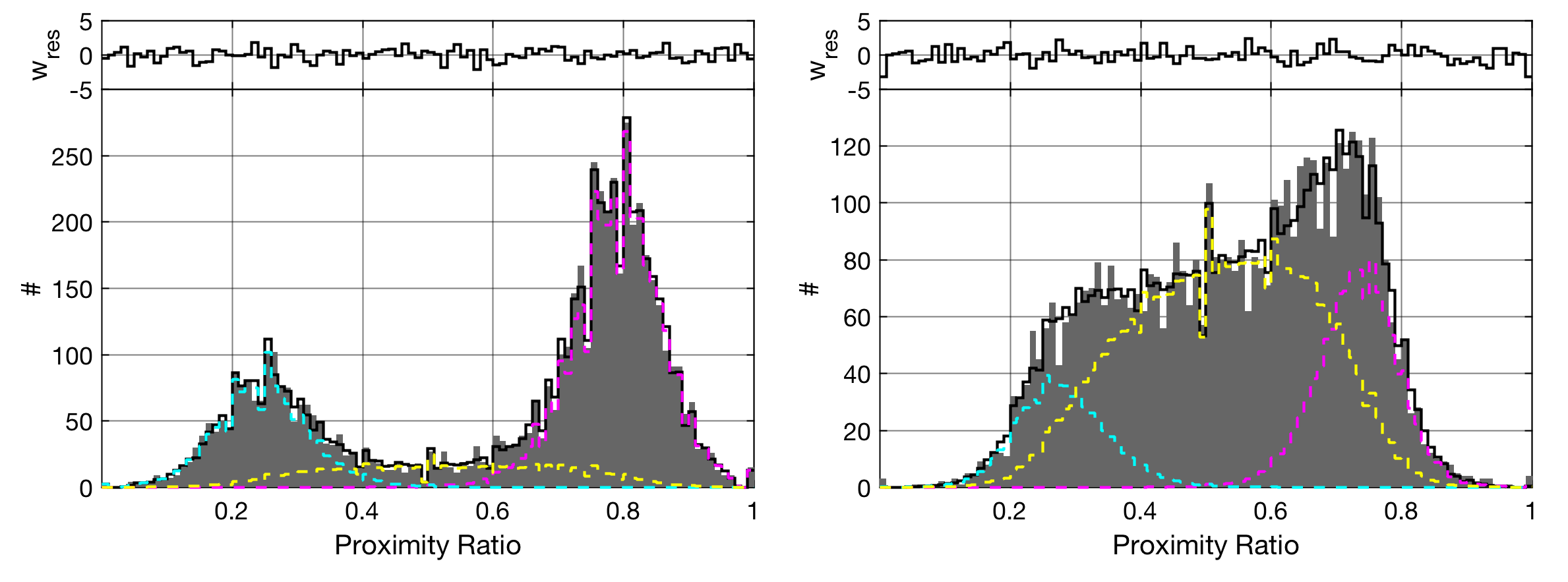
Dynamic interconversion between different FRET states leads to characteristic mixing of FRET efficiencies dependent on the rates of interconversion. This usually shows through the formation of a bridge between the FRET states in the histogram.
Dynamic-PDA, as described in [Kalinin2010a], can be activated by clicking the Dynamic Model checkbox in the Settings tab. This will enable a two-state kinetic model using the first two species of the fit model. The respective amplitudes in the fit parameter table will be changed to forward and backward rates \(k_{12}\) and \(k_{21}\) between the two states in unit of \(\textrm{ms}^{-1}\).
Currently, only the two-state model is implemented. Additional static populations can be added.
Note
It is recommended to globally fit a series of proximity ratio histograms generated at different time bins from the same measurement to obtain a higher accuracy in the determined rates.
Error estimation¶
PDAFit offers to options to estimate the confidence intervals of the fit parameters, available through the menu Fit -> Estimate Error.
- Estimate Error from Jacobian at solution:
- This option will use the Jacobian at the fit result to estimate the confidence intervals of the parameters.
- Estimate Error from Markov-chain Monte Carlo:
- This will perform a Markov-Chain Monte Carlo chain over the \(\chi^2\)-surface to estimate the confidence intervals of the parameters.
The output will be returned into the current workspace.
Background deconvolution¶
PDA can be used to describe a complete single-molecule FRET measurement without burst selection. In this case, many of the recorded time bins will only contain background signal and the resulting photon count distribution will be vastly different from the true distribution of fluorescence signal. See the section in the PAM manual for how to export a total measurement to PDA.
PDAFit implements the deconvolution method as proposed in [Kalinin2008] to recover the distribution of fluorescence signal from the observed photon count distribution using the know distribution of background counts.
This option only applies to the Histogram Library method.
Note
Only use this option when the total measurement is analyzed. This method does not apply for burst-selected data sets!
Program structure¶
Database Tab¶
Files that are loaded or added via the file menu are put into a list in the database tab. Files can be deleted from this list using the keyboard.
- Save:
- The list can be saved in a PDA Database File (.pab), so it can be opened at a later point in time. Importantly, the database file just contains a reference to the filename and path of all files in it.
- Load:
- Load a previously saved database list (.pab).
Fit Table¶
To remove a component from the fit model fix the amplitude A to 0. Unchecking a file’s ‘Active’ checkbox removes that file from analysis, but not from the database. Clicking an ‘All’ row cell value applies this value to all rows.
Settings Tab¶
The Settings tab allows you to set a number of parameters that affect the analysis and visualization. The options are explained in more detail in the respective sections. Here, an overview and brief description is given.
- Number of Bins:
- Specifies the number of bins used to construct the proximity ratio histogram over the interval [0,1]. This will effect the display of the histogram, and may effect the fit result of the Histogram Library and Monte-Carlo methods. The MLE method is unaffected by this setting.
- Minimum/maximum Number of Photons per Bin:
- Restrict the selection of time bins (see the respective section).
- Grid resolution for E:
- Defines the grid resolution over the apparent FRET efficiency for the Histogram Library method. The method will construct a library of shot-noise limited proximity ratio histograms at the grid values (e.g. at setting 100, at \(\epsilon\) = [0, 0.01, 0.02, …, 0.98, 0.99, 1]). It is not advised to set this value lower than 100. Increasing this value with increase the accuracy of the analysis at higher computational cost. This setting has no effect on the PDA methods MonteCarlo or MLE.
- Stoichiometry threshold:
- Set threshold to restrict the selection of time bins based on the stoichiometry parameter (see the respective section).
- PDA Method:
- Set the method for the PDA analysis between Histogram Library, MLE and MonteCarlo. See the respective section for details.
- Fit Method:
- Set the fit method to optimize the parameters. Choose between Simplex (fminsearch function), Gradient-based (using the fmincon or lsqnonlin function), Patternsearch or Gradient-based (global). See the MATLAB documentation for more explanation on these fit methods. Generally, the Simplex method yields good results at acceptable convergence time.
- MonteCarlo Oversampling:
- This parameter determines the oversampling when using the MonteCarlo method. Increasing this number will reduce the statistical noise in the simulated histogram at the cost of increased computation time. The other methods are not affected by this parameter.
- Chi2 method:
- Choose if the \(\chi^2\) goodness-of-fit estimator should be calculated based on Poissonian or Gaussian counting statistics.
- Fix Sigma at fraction of R:
- Check this to fix the distribution width \(\sigma\) at a fixed fraction of the mean distance of a species, i.e. \(\sigma = k * R\) where \(k\) is typically in the range between 0.05 to 0.2. Set the proportionality factor \(k\) using the edit box. The proportionality factor will by default be optimized by the fitting routine. You can additionally fix the proportionality factor to a custom value by checking the Fix? checkbox.
- Dynamic Model:
- Check this checkbox to enable dynamic-PDA. Only works in conjunction with the Histogram Library method. See the respective section for details.
- Deconvolute background:
- Performs deconvolution of the photon count distribution to obtain the background-free fluorescence photon count distribution. Use this only when fitting a whole measurement data set without burst selection. See the respective section for more details.
- Half global:
- Allow to set parameters global between subsets of the loaded measurements. Please inquire about details on how to use this functionality.
- Live plot update:
- Enabling this option will cause a live plot update during the fitting process. Note that this slows down the fitting since the plotting takes a significant amount of time. Use this option to check the status of the fitting routine, but generally leave it off.
- Ignore outer bins:
- This options ignores the outermost bins for the calculation of the \(\chi^2\) goodness-of-fit estimator, i.e. the bins [0,1/N] and [1-1/N,1] where N is the number of bins in the proximity ratio histogram. This option can be useful if large deviations between model and data are observed for these bins.
- gauss amplitude:
- Enabling this checkbox will scale distance distribution fit result plot with the respective amplitudes of the species. Disable this if you mainly want to investigate changes in the distance and not in the respective population sizes.
- Brightness correction:
- Corrects for brightness differences between different species using a donor-only brightness reference. This feature is untested and experimental.
| [Kalinin2012] | Kalinin, S. et al. A toolkit and benchmark study for FRET-restrained high-precision structural modeling. Nat Meth 9, 1218–1225 (2012) |
| [Antonik2006] | (1, 2, 3) Antonik, M., Felekyan, S., Gaiduk, A. & Seidel, C. A. M. Separating Structural Heterogeneities from Stochastic Variations in Fluorescence Resonance Energy Transfer Distributions via Photon Distribution Analysis. J. Phys. Chem. B 110, 6970–6978 (2006). |
| [Kalinin2010a] | Kalinin, S., Valeri, A., Antonik, M., Felekyan, S. & Seidel, C. A. M. Detection of structural dynamics by FRET: a photon distribution and fluorescence lifetime analysis of systems with multiple states. J. Phys. Chem. B 114, 7983–7995 (2010). |
| [Kalinin2008] | Kalinin, S., Felekyan, S., Valeri, A. & Seidel, C. A. M. Characterizing multiple molecular States in single-molecule multiparameter fluorescence detection by probability distribution analysis. J. Phys. Chem. B 112, 8361–8374 (2008). |
| [Kalinin2010b] | Kalinin, S., Sisamakis, E., Magennis, S. W., Felekyan, S. & Seidel, C. A. M. On the origin of broadening of single-molecule FRET efficiency distributions beyond shot noise limits. J. Phys. Chem. B 114, 6197–6206 (2010). |